レージです。
突然ですが皆さんは「72の法則」ってご存知ですか?
複利で運用した際に、資産が倍になるまでの年数をザックリ計算する法則のことで、
72÷(複利のパーセンテージ)
=(資産が倍になるのに必要な年数)
といったものです。
72という数字を割るので「72の法則」と呼ばれるのですね。
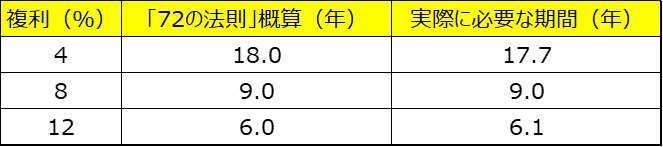
例えば、複利4%だったら72÷4=18なので18年、
複利8%だったら72÷8=9なので9年、
複利12%だったら72÷12=6なので6年、
といった具合に面倒な複利計算を簡単にザックリ計算できるのです。
実際の結果と比較すると割と精度で計算できていることが分かります。
この法則を聞いたとき「便利やなー」となった一方でこう思いました。
「あれ、複利72%の時って、72÷72=1だけど1年で倍になるって計算だけどおかしくない?
1年で倍にするには利率100%では…?
何かおかしいな…」

一体何がおかしいのでしょう…。
これってトリビアになりませんか?(古い)
ということで「72の法則」を大解剖してみました!(割と長編です)
発見(大げさ)
数式をこねくり回して得た発見を書きます。
興味がある方は導出過程も是非ご覧ください…!
(発見①)
72の法則より「69の法則」が妥当。
(発見②)
「年利72%で1年運用したら資産が2倍になる」というおかしな結論が出るのは、マクローリン展開において2次以上の微小量を無視したから。
(発見③)
「72の法則」では年率7.846%くらいまで運用成績を過小評価する(実際に必要な期間よりも長く見積もってしまう)。
(発見④)
資産がα倍になるまでの年数計算「パワたまの法則」
(72の法則の拡張)

例えば、複利4%で資産が5倍になる年数を概算したいとき、表から160という数字を確認して複利で年数を割れば…
160÷4=40。ザックリ40年必要と分かります。
(実際は約41年。悪くない精度です)
次章で一つ一つ検証していきます。
数式がそれなりに出てきますが、基本的には高校で習う対数関数の知識があれば問題ないかと思います。(一ヶ所だけ大学数学が登場しますが)
それではどうぞよろしくお願いいたします。
発見①「72の法則」より「69の法則」が妥当
「敵を知り己を知れば百戦危うからず」ということばもあるように(?)まずは「72の法則」とはなんぞや、というところから探っていきます。
いきなり抽象的な話をしても分かりづらいので、まずは具体例から…
200(円)を元本として、複利5%で運用するときを考えます。
この時の資産の推移は…
運用開始時点(0年目):![]()
1年目:
2年目: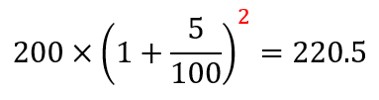
3年目: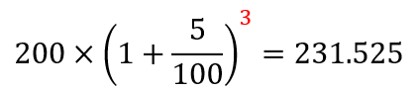
4年目: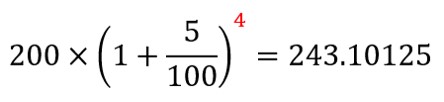
パターンが見えてきましたね。よってN年目の運用結果は
N年目: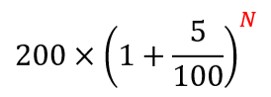
となります。
Nってなんやねん?(数学アレルギーの方向け)
昔から思ってたけどNってなんやねん、という方は「ポーカーでのジョーカー」・「ポケモンでいうところのメタモン」くらいに思ってもらえればと思います。要するに「なんにでもなれる」って奴です。
Nに好きな数字を入れると、なんにでも変身できるんですね。例えば、Nに3を放り込むと、たしかに3年目の運用成績と同じなることが分かります。
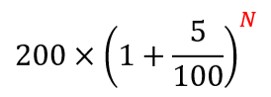
N=3
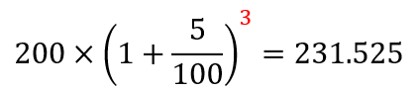
一つの数式だけですべてをカバーする…スマートですね。こういうのを数学では「一般化する」といいます。ちなみに、N=1やN=0の時も成立してます。
更に一般化します。
A(円)の元本を複利R(%)で運用した場合を考えます。資産推移は以下の通りです。上の5%での結果を「200→A、5→R」に置きかえるイメージですね。
運用開始時点(0年目):![]()
1年目: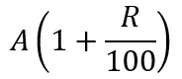
2年目: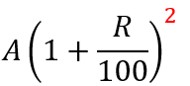
3年目: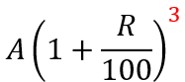
4年目: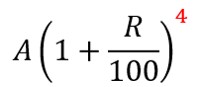
こちらもパターン丸見えですね、よって運用してN年後の資産額(円)は
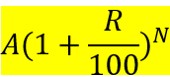
となるわけです。
この運用結果(上のハイライトした数式)が
元本の2倍(=2A)になるというのは
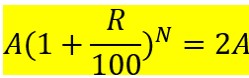
という方程式で表すことができます。
我々が関心があるのは「2倍になるまでの年数(=N)」を知りたいので、上の方程式をNについて解けばOKです。
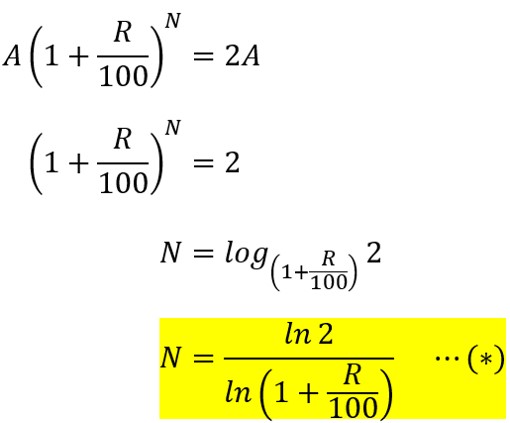
2行目から3行目への変形は「対数関数」の定義で書き換えただけですので、対数関数とか馴染みねえよという方は、「そう書くのね」と思っていただけたらと思います。あと厳密にはR=0, -100<Rでは成立しないです(しっかり書いてないと数学ガチ勢に怒られそうなので…)
3番目から4番目への変形は「底の変換公式」使っています。
また、”㏑”は自然対数です。
![]()
ごちゃごちゃ言いましたが、無事Nについて解けました。
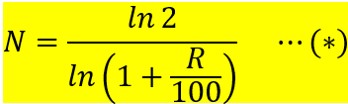
これが何を意味しているかというと(*)式の右辺が計算できれば、
「資産が2倍になるまでの年数N」を求めることができます。
ただ分母も分子もキモいので、それぞれ詳しく検証していきます。
まず分子の![]() ってなんやねん、
ってなんやねん、
という感じですがGoogle先生に聞けば値を教えてくれます。
(雑に言えば「ネイピア数2.71828…を何乗したら2になりますか?」というのを聞かれていると思ってください)
Google先生「はい、どうぞ」

はい、ということで
![]() です。
です。
(要は2.71828…を0.69314718056…乗したら2になるってことですね)
分子の計算が完了しました。
次に分母の計算をしたいのですが、結構手ごわいです。
いま、(*)式の分母に対してマクローリン展開**をすると、
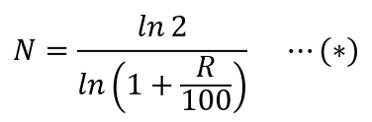
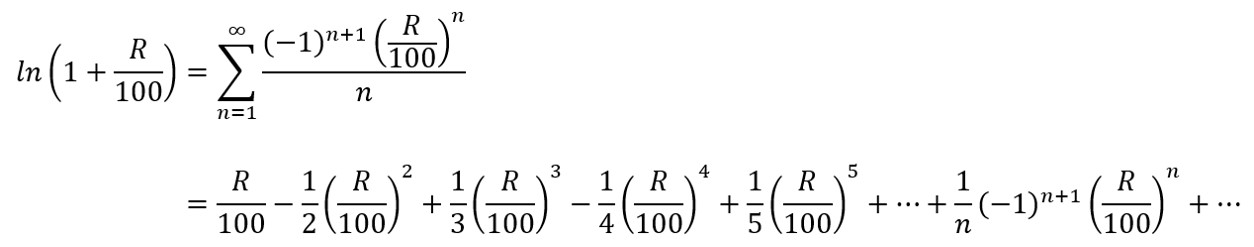
(厳密には複利の利回りRが、-100%以下or100%より大きいとこの式は成り立ちません。しっかり言わないと数学ガチ勢の方に怒られそうなので断っておきます…)
**マクローリン展開って?雑に言うと「なんかこの関数難しいから”簡単な関数いっぱい使って”部分的にものマネしようぜ」ということです。
今回でいえば、「自然対数」というよく分からん関数が扱いづらいので、2乗とか3乗という馴染みのある関数の足し算・引き算で表現することを意味します。
ちなみにΣ記号の意味は、(n=1の結果)+(n=2の結果)+(n=3の結果)+…というのをΣ記号上に書いてあるところまで続けるという意味しています(今回は∞と書かれているので、無限回足します)
雑すぎて流石に怒られそうなので、もうちょっとマクローリン展開をちゃんと言うと「(無限回微分可能な)ある関数f(x)をx=0の近傍にて、導関数の値から得られる項の無限級数で表す」といったところでしょうか。
数学ガチ勢の方がいらっしゃたらアレなので更に付け加えておくと、「自然対数![]() におけるマクローリン展開の収束半径が
におけるマクローリン展開の収束半径が![]() なので、複利の利回りRは-100%より大きく100%以下の範囲」としております。
なので、複利の利回りRは-100%より大きく100%以下の範囲」としております。
ちゃんと知りたい方は「マクローリンの定理」で是非ググってみてください。数式としてはこんな感じです。

さて、ここで、黄色でハイライトした第二項以降につき、
2次以上の微小量***のため無視すると、以下のように近似ができます。
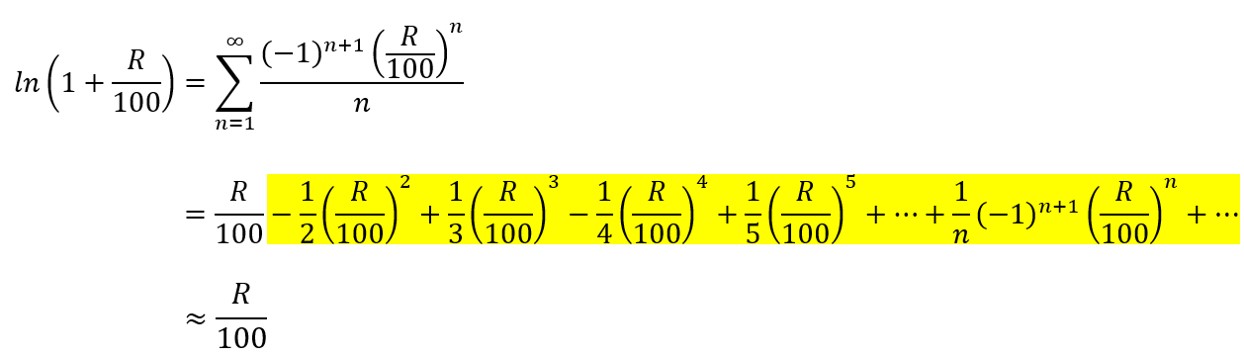
※ちなみに![]() は≒と意味同じです。かっこいいので
は≒と意味同じです。かっこいいので![]() にしました。笑
にしました。笑
***2次以上の微小量のため無視って?
雑に言えば「小さい数字を2乗したらめっちゃ小さくなるから無視してよくね?」、「3乗とかしたらめっっちゃ小さいし、2乗より後ろはガン無視してよくね?」ということです。
具体的に複利3%(R=3)の場合で見てみると、
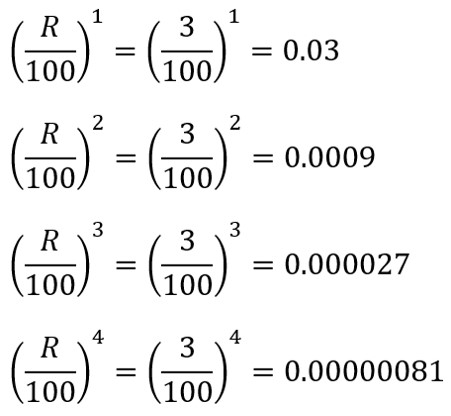
確かに2乗以降は初めの0.03に比べるとかなり小さい値になっています。
先ほどのマクローリン展開と照らし合わせると、
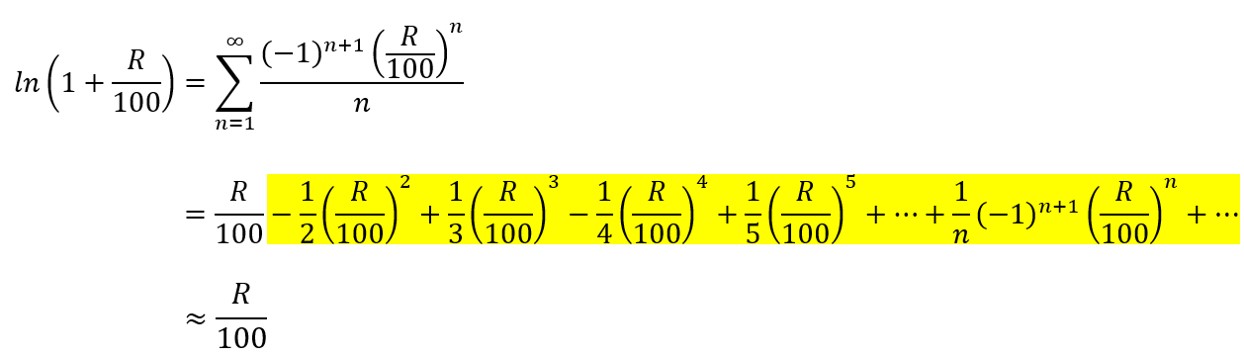
「このハイライト部分(次数が2次以上)って
第一項![]() に比べて小さいし、ガン無視しよっとw」
に比べて小さいし、ガン無視しよっとw」
これが「2次以上の微小量のため無視」したということです。
2次以上の微小量を無視した結果、(*)式は以下のように変形できます。
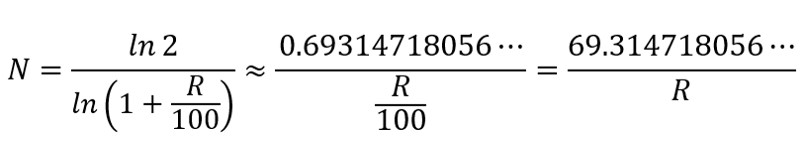
つまり、資産が倍になる年数Nを求めたければ、
69.314718056…を複利のパーセンテージRで割れば
ザックリ計算できる!ということを意味しています。
ただ、実用上69の割り算って若干面倒なので、
69に近く、且つ割り算もしやすい(=約数が多い)72が採用されています。
(←冒頭の発見①)
(発見①)72の法則より「69の法則」が妥当。
よって資産が倍になるのに必要な年数は
「複利のパーセンテージRで72を割れば概算できる」
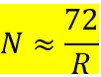
これが「72の法則」です。
発見②近似による現実とのズレ
「72の法則」を計算する過程で、2次以上の微小量を無視しました。
いったいこれで何が起きてしまうのでしょうか?
今一度数式を振り返ってみます。
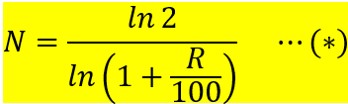
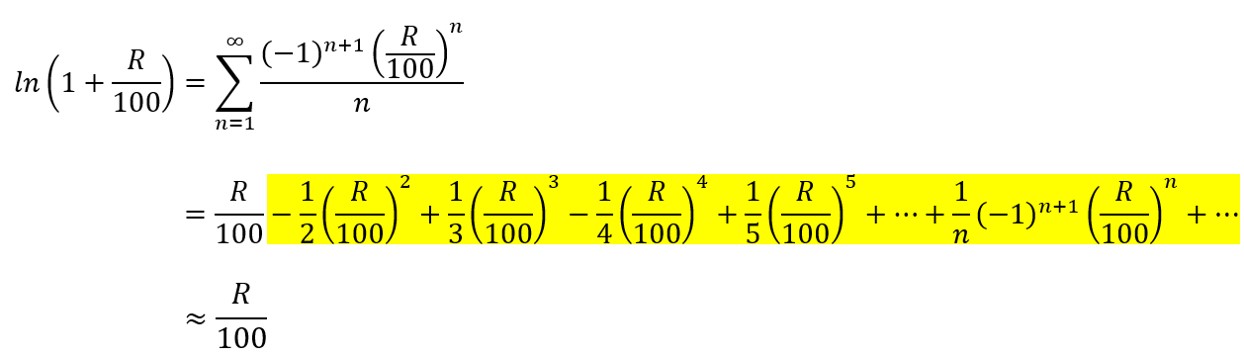
「2次以上の微小量を無視」により、要は引くべき値を引いていない(=分母を過大評価している)ということを意味します。
先ほどR=3%を例に挙げ、
「2次以上の微小量って小さいから無視していいよね」と説明しました。
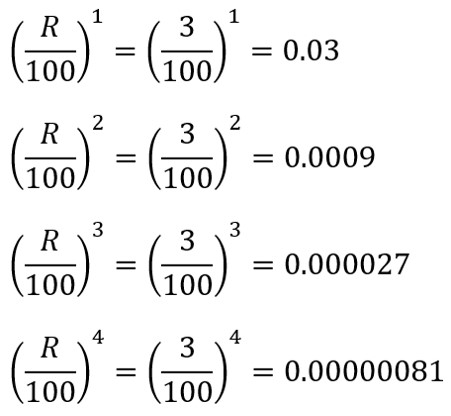
ではもっと運用利回りが大きい時、例えばR=90%の時はどうでしょうか。
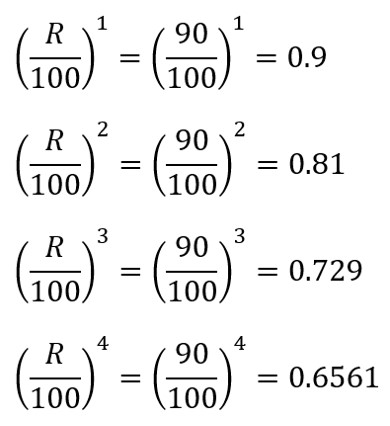
結論:2次以上の微小量、全然無視できないじゃん…
そうなんです。つまりRが大きいと(*)式の分母を過大評価してしまい、結果Nを実際よりも小さく見積もってしまうのです。
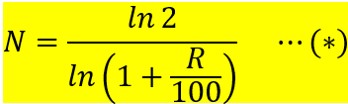
もっと平たく言うと、「72の法則」を使う際「運用成績Rが高くなるほど、資産が2倍になるまでの期間を短く見積もってしまう」ということです。
(←冒頭の発見②)
(発見②)「年利72%で1年運用したら資産が2倍になる」というおかしな結論が出るのは、マクローリン展開において2次以上の微小量を無視したから。
確かに、大きいRの時に短く見積もっていることが分かります。

発見③「72の法則」の信ぴょう性
「運用成績が高いほど運用期間を短く見積もってしまうことは分かった、じゃあ具体的に複利何%から短く見積もっちゃうの?」
気になりますよね?(私だけ?)
このトリビアの種、つまりこういうことになります。(古い)
資産が2倍になる期間 と
と
「72の法則」による概算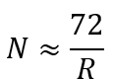 が一致するときのR、
が一致するときのR、
つまり方程式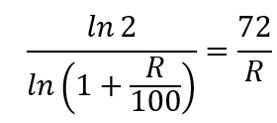 を満たすRは…?
を満たすRは…?
ということになります。
しかしこの方程式、残念ながら解析的に解けません(私の数学力が足りないだけかもしれないです…。ガチ勢の方、お知恵を拝借できたら幸いです…)
ということで、大学受験でもおなじみの手法
「グラフを書いてみる」作戦に持ち込んでみます。
以下のような関数f(R)を準備します。
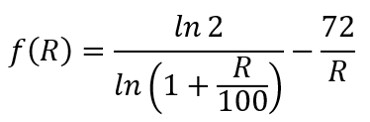
関数f(R)は「(資産が2倍になる期間)と(72の法則で計算される期間)の差」を表しているので、
f(R)の値がマイナスでであれば、「72の法則」で求めた期間の方が長いことを意味しているので、複利の運用成績を過小評価していることになります。
同様に、f(R)の値がプラスであれば、「72の法則」で求めた期間の方が短いことを意味しているので、複利の運用成績を過大評価していることが分かります。
そして、f(R)=0の時、これは「72の法則」で求まる期間が実際の期間とピッタリ一致していることを意味するので、この時のRを探すのが、まさに方程式
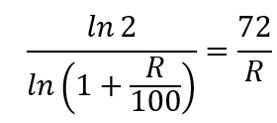
を解くこと意味します。
これにて方程式を解く問題が、
「f(R)のグラフを書いて軸との交点のRを読み取る問題」に帰着しました。
ということで以下が関数f(R)のグラフです。
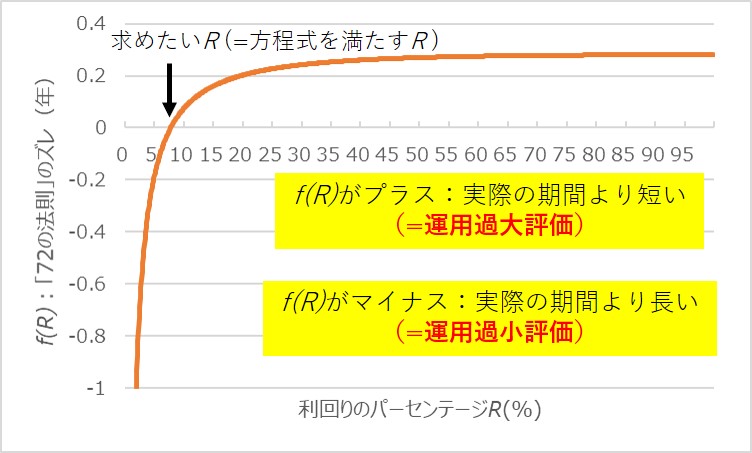
見たところRが5から10の間くらいに方程式の解がありそうです。(厳密にはf(R)の単調増加性を示す必要がありますが、今回は勘弁してください、数学ガチ勢の皆さん。)
Rが5~10の部分を拡大してみました。R=8%くらいが解っぽいですね。

だいぶ見えてきました、R=7.85%付近ですね。もうひと拡大します。
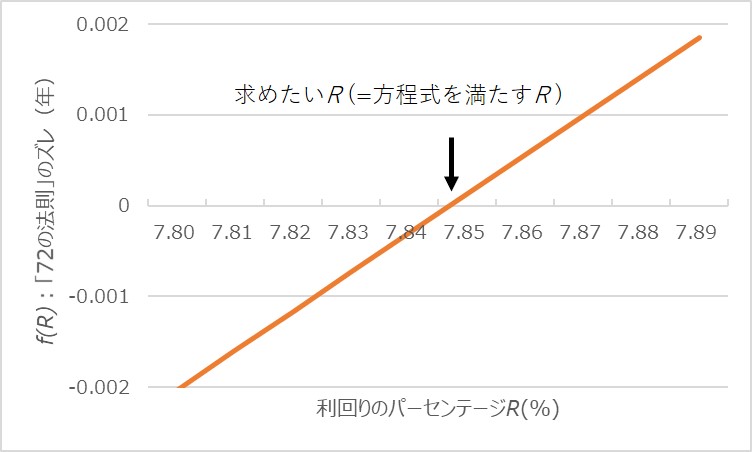
ここまでくれば大分精度のある方程式の解が得られそうですね。この区間におけるRと対応するf(R)の値を表にしました。
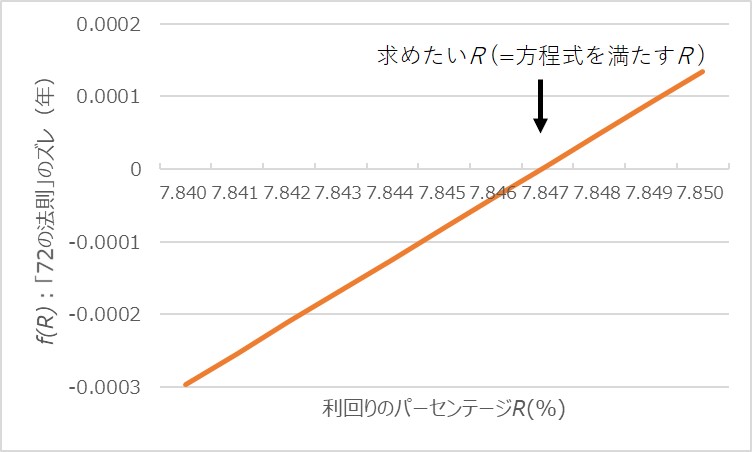
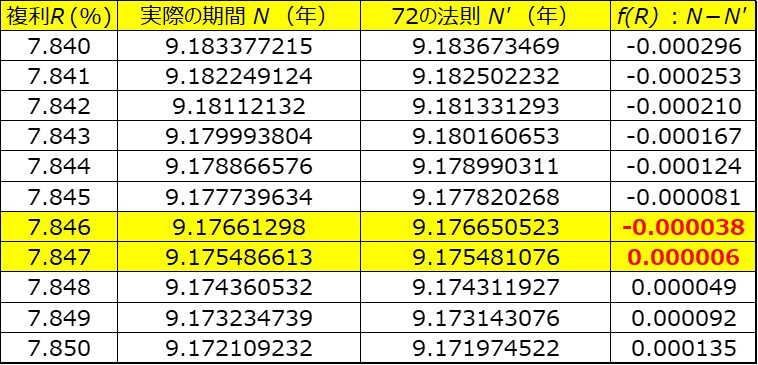
R=7.846%の時f(R)がマイナス(=運用結果を過小評価)だったのが、
R=7.847%ではf(R)がプラス(=運用結果を過大評価)になってます。
すなわち方程式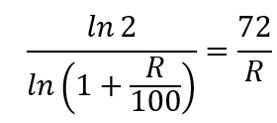
の解はRが7.846%~7.847%のどこかということが分かりました。
(発見③)「72の法則」では年率7.846%くらいまで運用成績を過小評価する(実際に必要な期間よりも長く見積もってしまう)。
発見④パワたまの法則(72の法則の拡張)
「72の法則って便利だけど、2倍になる期間しか計算できないの?」
「俺は資産を100倍したいんだ!100倍までかかる時間を教えろ!」
そんな声が聞こえてきます(幻聴)
それを叶えるのが「パワたまの法則」です。
(自分の名前がついた法則、夢だったんですよね笑)
さて、資産が2倍になるまでの期間は(*)式で表されていました。
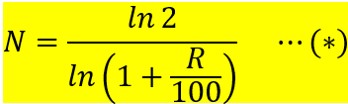
「資産がα倍になるまでの期間N’」を求めるには、
(*)式のNをN’に、2をαに変えればよいので、
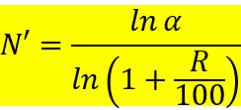
という式が得られます。
以降は「72の法則」の時同様に、
分母をマクローリン展開して近似をすれば、
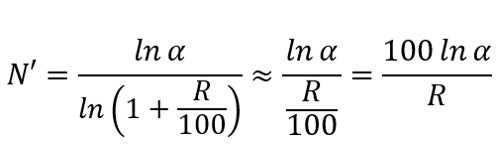
よって、資産がα倍になるまでの期間N’を求めるための式が得られました。
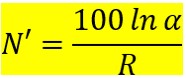
上の数式にあるαに好きな数字を代入することで、
以下の表を得ることができます。

これらの数字を複利のパーセンテージRで割れば、資産がα倍に年数を概算することができます。そうとはいっても、これらの数字を割り算するのが面倒なので、±3の範囲で最も約数が多い(=割り算がしやすい)数字で置き換えます。(「72の法則」も本来であれば「69の法則」でしたね。)
これにより、「パワたま」の法則が得られました!
(←冒頭の発見④)

α=2の時(資産が2倍になる時)、
「パワたまの法則」と「72の法則」が一致します。
本当に「パワたまの法則」って使えるの?という方のために、
複利R=4%, 8%, 12%の3パターンでシミュレーションしました。
概算にしては割といい精度だと思います。
複利R=4%の時

複利R=8%の時

複利R=12%の時

さいごに
長文お付き合いいただき本当にありがとうございました。
巷で言われている便利な法則を使うだけでなく、
実際に手を動かして自ら検証してみると色々な発見がありますね。
最後に今回の発見を再掲して締めたいと思います。
最後までありがとうございました!
(発見①)
72の法則より「69の法則」が妥当。
(発見②)
「年利72%で1年運用したら資産が2倍になる」というおかしな結論が出るのは、マクローリン展開において2次以上の微小量を無視したから。
(発見③)
「72の法則」では年率7.846%くらいまで運用成績を過小評価する(実際に必要な期間よりも長く見積もってしまう)。
(発見④)
資産がα倍になるまでの年数計算「パワたまの法則」
(72の法則の拡張)



